Quienes estudian matemáticas vieron en algún momento la teoría de los conjuntos, esos círculos conteniendo distintos elementos o números, que se podían unir, intersectar y tenían muchas propiedades.
Sin embargo, pocos sospecharon o entendieron que esos dibujos elementales conforman una herramienta base del razonamiento matemático y lógico, al punto que toda la matemática moderna (álgebra, geometría, probabilidad, funciones, lógica) se puede expresar en términos de conjuntos, lo que permite organizar información y trabajar con datos. El concepto de conjunto se utiliza en el campo de la probabilidad y la estadística, la informática y la ciencia, entre tantísimos otros.
En particular, fue esta teoría la que permitió uno de los logros más impactantes de la historia de la matemática, el cual obligó a modificar la mirada que hasta entonces se tenía sobre el infinito, un tema con el cual nadie quería lidiar demasiado.
Fue Georg Ferdinand Ludwig Philipp Cantor (1845-1918), matemático alemán, el responsable de cambiar para siempre la forma en que se piensa y se considera al infinito, al demostrar, matemáticamente, que a pesar de que todos los infinitos son infinitos, algunos son más grandes que otros. Este concepto de “distintos infinitos” o infinitos de diferente tamaño, fue completamente impactante para la ciencia de los números.
Los números Aleph (ℵ) lo utilizó Candor para representar el tamaño de un conjunto infinito, acompañado de un 0, un 1, un 2, etc. Es la primera letra del alfabeto hebreo y simboliza la unidad. Su forma es la representación de la cabeza de un buey.
Para llegar a esa idea, Cantor trabajó relacionando distintos conjuntos y exploró el infinito de manera rigurosa analizando diferentes colecciones de elementos. Así, el infinito dejó de ser una idea filosófica vaga, para convertirse en algo que podía estudiarse. En ese camino, Candor planteó una situación insólita: ¿Tienen el mismo “tamaño” todos los conjuntos infinitos? Lo que parecía tener una respuesta obvia, positiva, terminó con una conclusión revolucionaria.
Nadie debería poder expulsarnos del paraíso que ha creado Cantor para nosotros. David Hilbert
Cantor comenzó por comparar dos conjuntos de números mdash;los naturales y los paresmdash; para establecer si, pese a ser ambos infinitos, eran equivalentes en tamaño.
Tanto los números naturales 𝑁 (1, 2, 3, 4…) como los números pares (2,4, 6, 8…) son conjuntos infinitos. Aunque pareciera que los pares son menos, Cantor mostró que ambos tienen la misma cantidad de elementos desde el momento que se puede hacer una correspondencia uno a uno entre los componentes de uno y otro conjunto. A ese tamaño de infinito Cantor lo llamó ℵ0>/sub> (Aleph-cero).
También llegó a esa conclusión cuando tomó los números racionales (los que se pueden expresar como fracción), otro ℵ0>/sub>. Es decir, tres conjuntos infinitos de igual tamaño.
Pero la cuestión cambió cuando incorporó el conjunto de los números reales 𝑅 (es decir todos los números, naturales, racionales, irracionales). Al compararlo con los naturales estableció que el de los reales resulta más grande: es un infinito mayor.
Para su teoría, Cantor definió al número transfinito, utilizado para medir los distintos tamaños de infinitos. Los llamó así porque van “más allá” de lo finito.
Cantor demostró eso mediante el denominado argumento de la diagonal, un mecanismo de su creación que le permitió verificar que para este caso no existe una correspondencia “uno a uno” entre los componentes de los conjuntos.
En particular, los números reales conforman un infinito mayor, más vasto, que el de los naturales. Ambos son infinitos, pero no del mismo tipo. Mientras que los naturales se pueden enumerar uno a uno mdash;según Cantor: tienen cardinalidad ℵ0>/sub>, el menor tipo de infinito posiblemdash;. Los reales no se pueden enumerar de esa manera, no existe una lista completa: los reales son innumerables.
Haber establecido que no todos los infinitos son iguales tuvo consecuencias enormes en la matemática. Por un lado, el infinito dejó de ser una idea filosófica o teológica para pasar a ser medible, lo cual abrió un terreno nuevo en la teoría de conjuntos, el cual hoy es la base del análisis, la topología, la lógica y gran parte de la matemática moderna. Permitió comprender mejor las funciones, los límites y la continuidad e influyó en la teoría de la computación y en los problemas de decidibilidad.
Abrió además la hipótesis del continuo, que plantea si existen un conjunto cuyo tamaño sea mayor que el de los naturales, pero menor que el de los reales, un “infinito intermedio”. Es una pregunta todavía abierta: que exista o que no exista es matemáticamente posible.
Me imagino un conjunto como un abismo. Georg Cantor
Meterse con el infinito no es un tema menor, sea desde la matemática, la filosofía o la ciencia. Muchos lo han considerado un monstruo, que llevaba siglos aterrorizando la lógica, las matemáticas y la filosofía.
Después de Cantor, los matemáticos han admitido que la existencia de un determinado objeto matemático puede estar garantizada aunque no se especifique cómo se puede construir.
Cantor inició un proceso caracterizado por la aparición de pruebas de existencia de un objeto desde la lógica.
Pero también en esa ardua y agotadora tarea, perdió parte de su cordura. O al menos eso instalaron quienes no comulgaban con sus ideas.
Más allá de su genialidad, Cantor debió soportar embates personales por sus ideas, y muchos utilizaron para desautorizarlo un hecho no menor: su supuesta demencia, una situación de salud que lo llevaba a sufrir períodos depresivos con internaciones psiquiátricas. A partir de 1899 fue internado en clínicas cada dos o tres años, aquejado de manías persecutorias y depresivas.
Muchos matemáticos de época aprovecharon esta situación para descalificarlo. Hasta hoy no hay elemento alguno que permita relacionar los estudios de Cantor con su enfermedad mental, mucho menos que la misma fue provocada por su obsesión por desentrañar los misterios del infinito.
Bertrand Russell, a quien Cantor contactó en 1911, publicó en 1967 una referencia a dos cartas que este le envió y a su comportamiento “un tanto excéntrico”. “Cantor fue uno de los mejores cerebros del siglo y a nadie sorprenderá saber que estuvo buena parte de su vida en un asilo para lunáticos”.
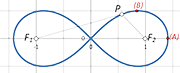
El “ocho acostado” que simboliza al infinito fue establecido en 1656 por John Wallis. Es, por su forma, una lemniscata, y representa a las cantidades sin límite. Se cree que el diseño se inspiró en el ouroboros, una serpiente que se come su propia cola y representa la eternidad.
El historiador Ivor Grattan-Guinness escribió en 1971: “Las cartas de Cantor a Russell tienen un carácter errático. Muestran varios de los hábitos que Cantor tenía cuando la agitación se apoderaba de él. Los renglones tienden a irse hacia arriba y no sólo continúan en los márgenes: en una página llegó a escribir de arriba a abajo y hay incluso un párrafo escrito en el dorso del sobre”.
Es posible que la enfermedad de Cantor tuviera causas genéticas, algo que no se pudo verificar en su época. Los ataques empezaban de repente con fases de excitación y exaltación. Finalizaban también de repente y los seguía la fase depresiva, durante la cual pasaba en silencio horas y horas. Finalizada esa etapa, volvía a su trabajo.
Lo que pocos dudan es que los cuestionamientos de sus pares y la tensión de su trabajo con el infinito pudiesen agudizar un poco más esas crisis.
La vida finita
Desde 1878 Cantor batalló además buscando demostrar la hipótesis del continuo. Fueron años de esfuerzo intenso. Y si esa hipótesis fue perturbadora para su estabilidad emocional, no lo fue menos la tragedia que sufrió en 1899 cuando Rudolf, uno de sus seis hijos, murió a los 13 años de edad.
En 1917, con 72 años de edad, Cantor ingresó al manicomio de Halle, en Alemania. Arrastraba además los efectos de la escasez de alimentos por la primera guerra mundial. Fue presa, además del cansancio y la enfermedad, del hambre. Murió el 6 de enero de 1918, de un ataque al corazón. Fue enterrado en Halle, cerca de la tumba de su hijo Rudolf.
Hoy Cantor es reconocido como un revolucionario de la matemática. En la cultura contemporánea, su nombre se asocia a su idea de que el infinito no es único, una noción acertada que continúa fascinando a matemáticos, filósofos y artistas por igual.